电影评论的情感极性分析

发表于 | 分类于 ， ，

这一节我们将使用Keras构建一个用于分析情感极性的神经网络模型，我们使用的是IMDB数据集，其中包含了50000条严重两极分化的评论。我们将从数据的准备开始，一步一步地讨论深度学习的实践方法论。

数据准备

Keras内置了下载IMDB数据的接口，但由于网络权限的原因，我们采用浏览器事先从网络上下载IMDB数据，把它放到我们的工程的corpus目录下，并在调用接口时指定加载数据的路径（注意一定要使用绝对路径）。该接口直接以元组的形式返回了(训练数据, 对应标签)以及(测试数据, 对应标签)。

1
2
3
4
from keras.datasets import imdb

(train_data, train_labels), (test_data, test_labels) = 
			imdb.load_data(path="/ABS_PATH/imdb.npz", num_words=10000)

参数num_words=10000表示仅保留训练数据中前10000个常出现的单词，较低频的词将被舍弃掉。

1
print(train_data[0], train_labels[0])
[1, 14, 22, 16, ..., 5345, 19, 178, 32] 1

我们分别输出一条训练数据与对应的标签，可以看出每条评论被表示为单词的索引编号的序列，而标签对应于0/1的整数表示负面（negative）与正面（positive）。显然，用单词索引编号序列表示的每条评论数据是不等长的，并不能用作神经网络的输入，我们需要将其转换为张量。一种最简单的张量转换方法就是one-hot编码，这种方法把每一条评论对应为一个词汇表大小的向量，出现过单词多对应的位置被置为1，其他位置为0。

1
2
3
4
5
6
7
8
9
10
11
import numpy as np

def vectorize_sequences(sequences, dimension=10000): #维数就是词汇表的大小
    results = np.zeros((len(sequences), dimension)) #创建样本数*词汇表大小的零矩阵
    for i,sequence in enumerate(sequences):
        results[i, sequence] = 1.
    return results

x_train = vectorize_sequences(train_data) #对训练数据进行one-hot编码
x_test = vectorize_sequences(test_data) #对测试数据进行one-hot编码
print(x_train[0])
[0. 1. 1. ... 0. 0. 0.]

当然，对应的标签也应该向量化作为神经网络的目标值，只需要将它们转换为Numpy数组就行：

1
2
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')

至此，我们完成了数据的准备工作，受益于使用了Keras的内置函数，我们省去了自行对数据进行训练集与测试集的划分。对于输入神经网络的数据，我们需要将它们都向量化。

构建网络

我们设计这样一个网络，它包含两个中间层，每一层都有16个隐藏单元；第三层输出一个标量，预测当前评论的情感，这个值在0~1的范围内，越接近0表示负向极性，越接近1表示正向极性。

1
2
3
4
5
6
7
from keras import models
from keras import layers

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

一个隐藏单元是对应的层所拥有的表示空间的一个维度，我们设计的中间层相当于做了这样一个运算：

output = relu(dot(W, input) + b)

其中W是一个形状为(input_dimension, 16)的权重矩阵，与W做点积相当于将输入数据投影到一个16维的表示空间中，再加上一个偏置变量b，为了让变换后的表示空间具有更多样性，把点积与相加后的线性变化结果输入relu激活函数进行一定的非线性变换。

然后，我们选择二元交叉熵损失函数与RMSprop优化器来配置模型，并且监控精度。

1
model.compile(optimizer='rmsprop', loss='binary_crossentropy', metrics=['accuracy'])

验证方法

为了在训练过程中监控模型在前所未见的数据上的精度，我们需要从训练数据中拨出一部分样本作为验证集，我们简单地选择前10000条。

1
2
3
4
5
x_val = x_train[:10000]
partial_x_train = x_train[10000:]

y_val = y_train[:10000]
partial_y_train = y_train[10000:]

现在可以开始训练了，我们让512个样本组成一个小批量，将模型训练20个轮次。

1
2
history = model.fit(partial_x_train, partial_y_train, 
		epochs=20, batch_size=512, validation_data=(x_val, y_val))
Train on 15000 samples, validate on 10000 samples Epoch 1/20 15000/15000 [==============================] - 7s 482us/step - loss: 0.4977 - acc: 0.7947 - val\_loss: 0.3720 - val\_acc: 0.8717 ... ... ...
Epoch 20/20 15000/15000 [==============================] - 3s 225us/step - loss: 0.0068 - acc: 0.9990 - val\_loss: 0.7058 - val\_acc: 0.8653

20次的迭代很快就完成了，fit()函数执行后返回一个History对象，该对象有一个history成员，它是一个字典，包含了训练过程中的相关数据。

1
print(history.history.keys())
dict\_keys(['val\_loss', 'val\_acc', 'loss', 'acc'])

我们使用Matplotlib在同一张图上绘制训练损失与验证过程中监控的指标，从图上直观地观察模型的表现。首先，绘制训练损失与验证损失:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import matplotlib.pyplot as plt

history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']

epochs = range(1, len(loss_values) + 1)

plt.plot(epochs, loss_values, 'bo', label='Training loss')
plt.plot(epochs, val_loss_values, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()

png

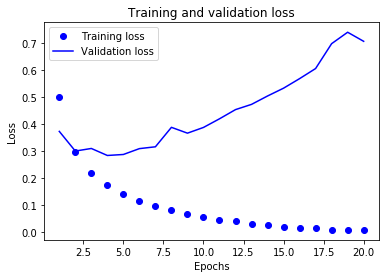
接着，我们再来绘制训练精度与验证精度：

1
2
3
4
5
6
7
8
9
10
11
plt.clf()
acc = history_dict['acc']
val_acc = history_dict['val_acc']

plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()

png

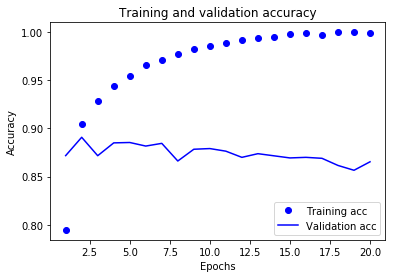
图中反应训练数据的折线走势与我们的预期是一致的，训练损失每轮都在降低，训练精度每轮都在提升；但是，验证数据的折线并不是这样，验证损失和验证精度似乎在第四轮达到了最佳值。也就是说，我们的训练过程从第五轮后就出现了过拟合：模型在训练数据上的表现越来越好，但在前所未见的数据上并没有这样的表现。为了避免过拟合，我们把模型训练的轮数设置为4，从头重新训练这个网络，并在测试集上进行评估。

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np
from keras import models
from keras import layers
from keras.datasets import imdb

(train_data, train_labels), (test_data, test_labels) = 
	imdb.load_data(path="/ABS_PATH/imdb.npz", num_words=10000)


def vectorize_sequences(sequences, dimension=10000):
    results = np.zeros((len(sequences), dimension))
    for i,sequence in enumerate(sequences):
        results[i, sequence] = 1.
    return results

x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)
                                                                      
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(optimizer='rmsprop', loss='binary_crossentropy', 
	metrics=['accuracy'])

history = model.fit(partial_x_train, partial_y_train, epochs=4, batch_size=512,
                   validation_data=(x_val, y_val))

results = model.evaluate(x_test, y_test)
print(results)
Train on 15000 samples, validate on 10000 samples Epoch 1/4 15000/15000 [==============================] - 7s 481us/step - loss: 0.5084 - acc: 0.7813 - val\_loss: 0.3798 - val\_acc: 0.8681 ... ... ...
Epoch 4/4 15000/15000 [==============================] - 6s 396us/step - loss: 0.1751 - acc: 0.9438 - val\_loss: 0.2840 - val\_acc: 0.8831 25000/25000 [==============================] - 6s 260us/step [0.3068919235897064, 0.87496]

很激动吧，我们仅仅用了不到三十行代码就到达了87%的精度，如果我们换用更复杂的模型，会有更好的结果。

总结

我们把这个实例的实践步骤总结一下，可以作为我们进行深度学习建模的方法论，按部就班地开展相关的实验与工程：

  1. 数据处理：划分训练集与测试集，把数据转换为适合输入神经网络的张量形式
  2. 构建网络：按照业务的具体需求，选择合适的网络结构、损失函数与优化器，构建一个完整的网络模型
  3. 验证方法：从训练集中拨出一部分数据作为验证集，将训练集与验证集同时放入fit()函数，指定相关的观测值，用训练记录绘制相关指标在训练集与验证集上的表现图
  4. 调整模型：根据表现图调整模型的超参数（如：迭代轮数、网络复杂度）或设计一定的正则化策略
  5. 固化系统：把性能最好的网络结构、参数用来训练最终的模型，固化为系统，并用测试集进行评测